Микроскопические методики в арсенале биолога 

Микроскопические методики имеют целью визуализацию событий, как статических, дающих представление о том «как устроено», так и динамических, отвечающих на вопрос «как реализуется функция». В арсенал микроскописта в широком смысле слова входят самые разные микроскопы, а изучают они результат взаимодействия света с объектом исследования. Таким образом, целесообразно разобраться последовательно в свойствах света и вариантах устройства микроскопов.

Итак, свет:

1. электромагнитная волна. Длина волны видимого света для человека находится в диапазоне 380-760 нм, что объясняется чувствительностью его зрительных пигментов. Скорость распространения света в вакууме равна около 300000 км/c. Отношение скоростей распространения света в вакууме и конкретной среде называется индексом рефрактивности данной среды.
2. имеет двойственную природу – корпускулярно-волновая природа света

Для наглядной демонстрации и объяснения множества феноменов взаимодействия света с веществом удобно воспользоваться принципом Гюйгенса, который состоит в том, что свет, доходя до любой точки пространства, превращает ее в источник вторичных сферических волн, огибающая которых определяет вектор распространения света в следующий момент времени.

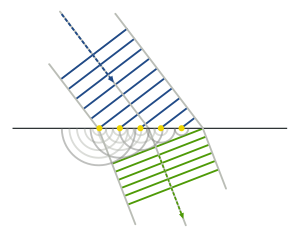
В данном случае крайняя левая точка становится источником вторичных волн раньше, чем крайняя правая точка, в результате чего огибающая вторичных волн – вектор распространения света меняет направление.

Добавление к этому принципу амплитудных и фазовых характеристик света, как это предложил Фреснель, позволяет объяснить так называемые интерференцию и дифракцию. Интерференция – это сложение волн, имеющих одинаковую фазу и вычитание противофазных волн

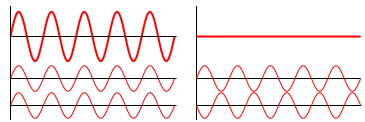
В результате интерференции вторичных волн при прохождении через отверстие возникает так называемая «дифракционная картина», характеризующаяся наличием минимумов и максимумов интенсивности.

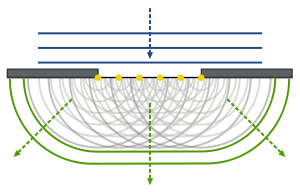
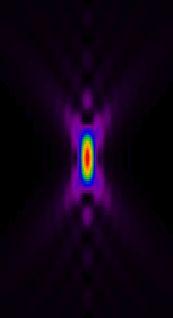
В случае прохождения света от точечного источника через линзу дифракционная картина выглядит как центральный диск максимальной интенсивности и серия концентрических колец - максимумов более низкого порядка, которая названа в честь английского астронома и математика Airy. В случае увеличения цифровой апертуры объектива величина центрального диска Айри уменьшается, а разрешающая способность такой системы увеличивается.

Функция распределения интенсивности светового потока от точечного источника в пространстве называется Point spread function – функцией рассеивания. Эта функция определяет расхождение между реальным объектом и объектом, изображение которого формируется оптической системой. Наличие у оптической системы сферической и хроматической аббераций вследствие несовершенства линз приводит к тому, что функция светорассеяния по глубине объекта имеет более сложный характер, само же рассеивание превышает таковое в плоскости XY. Следствием этого является меньшее разрешение оптической системы по оси Z по сравнению с осями X и Y.

 

Поскольку реальный объект – есть некоторая совокупность светящихся точек разной интенсивности, то формируемое изображение – результат сложения функций рассеяния с совокупности условных точек, составляющих объект. Данное сложение называется конволюцией. Таким образом, для микроскопического изображение требуется коррекция, учитывающая отклонение светящейся точки от ее изображения в оптической системе. Данная процедура извлечения реального изображения из мнимого называется деконволюцией.

При этом в случае деконволюции PSF различных оптических систем различаются и можно руководствоваться теоретической PSF, а можно провести ее экспериментальное определение на реальном микроскопе, что учтет особенности конкретной оптической системы.

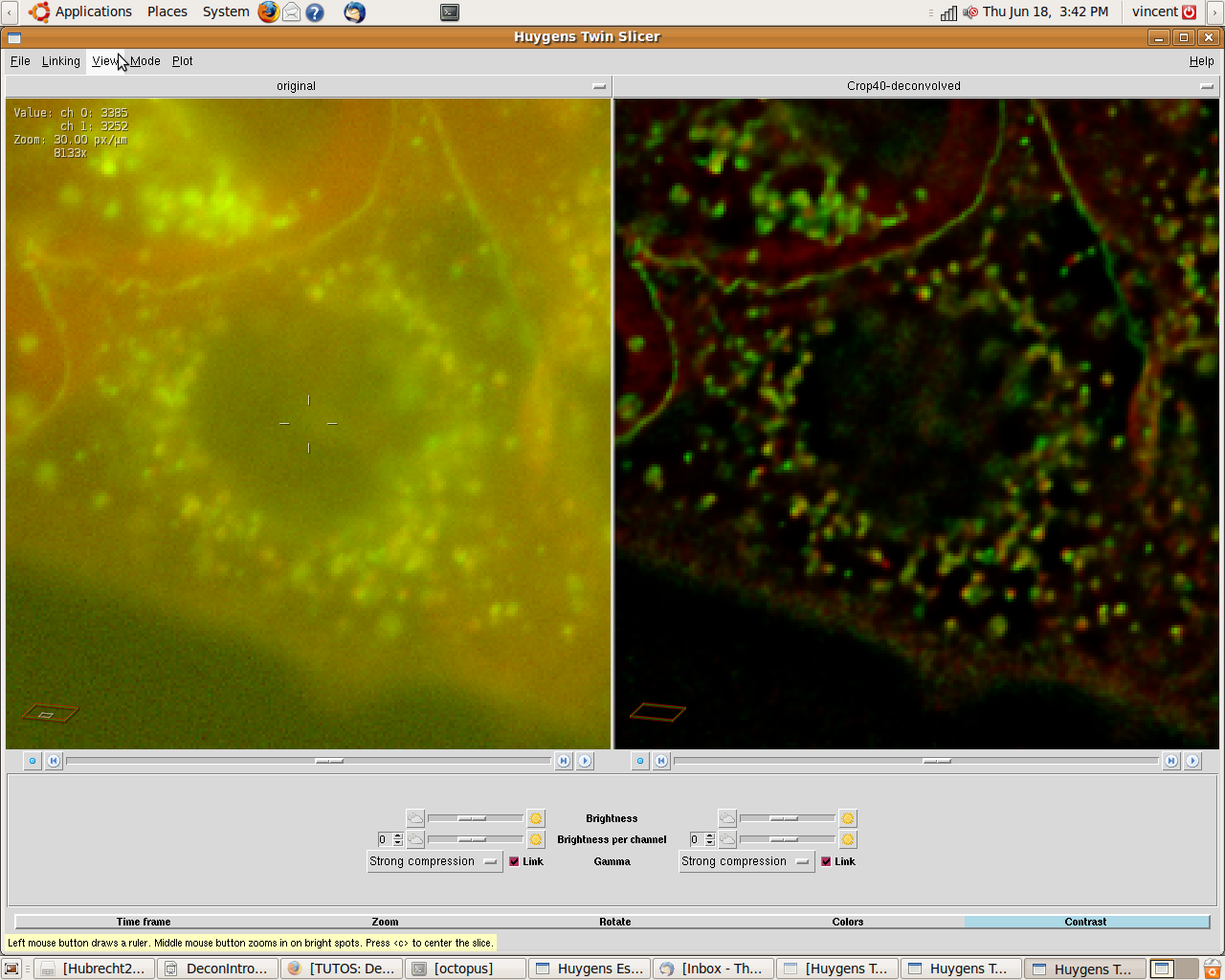
Практические примеры (слева – исходное изображение, справа – после деконволюции). Стоит отметить, что деконволюция необходима как для изображений, полученных на обычных, так и на флуоресцентных и конфокальных микроскопах. В нашем каталоге различные методы обработки изображений, включая алгоритмы деконволюции, Вы можете найти в разделе «Программы для микроскопии» - Huygens, SVI, а также Imaris, Bitplane

Изображения взяты с сайта компании SVI и их любезного разрешения